انواع مرتب سازی

برای دیدن انواع مرتب سازی به ادامه مطلب بروید.

مرتب‌سازی حبابی

از ویکی‌پدیا، دانشنامهٔ آزاد

(تغییرمسیر از مرتب سازی حبابی)

پرش به: ناوبری، جستجو

مرتب‌سازی حبابی (به انگلیسی: Bubble sort)‏ یک الگوریتم مرتب‌سازی ساده‌است که فهرست را پشت سرهم پیمایش می‌کند تا هر بار عناصر کنارهم را با هم سنجیده و اگر در جای نادرست بودند جابه‌جایشان کند. دراین الگوریتم این کار باید تا زمانی که هیچ جابه‌جایی در فهرست رخ ندهد، ادامه یابد و در آن زمان فهرست مرتب شده‌است. این مرتب‌سازی از آن رو حبابی نامیده می‌شود که هر عنصر با عنصر کناری خود سنجیده‌شده و درصورتی که از آن کوچک‌تر باشد جای خود را به آن می‌دهد و این کار همچنان پیش می‌رود تا کوچک‌ترین عنصر به پایین فهرست برسد و دیگران نیز به ترتیب در جای خود قرار گیرند (یا به رتبه‌ای بالاتر روند یا به پایین تر فهرست رانده شوند.) این عمل همانند پویش حباب به بالای مایع است.

این مرتب‌سازی از آن رو که برای کار با عناصر آن‌ها را با یکدیگر می‌سنجد، یک مرتب‌سازی سنجشی است.

با فرض داشتن n عضو در فهرست، در بدترین حالت 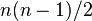عمل لازم خواهد بود.

عملکرد

بدترین زمان اجرا و پیچیدگی متوسط مرتب سازی حبابی هر دو (O(n^2 می‌باشند که در آن n تعداد عناصری است که باید مرتب شوند.
الگوریتم‌های مرتب سازی بسیاری وجود دارند که بدترین زمان اجرای آنها از این بهتر است یا پیچیدگی متوسط آنها (O(nlgn است. حتی بقیه اگوریتم‌های مرتب سازی از (O(n^2 مثل مرتب سازی درجی، عملکرد بهتری نسبت به مرتب سازی حبابی از خود نشان می‌دهند.

خرگوش‌ها و لاک پشت‌ها

در مرتب سازی حبابی موقعیت عناصر درون فهرست نقش بسزایی در تعیین عملکرد آن دارد. از آنجایی که عناصر بزرگ در ابتدای فهرست به سرعت جابجا (swap) می‌شوند، مشکل چندانی در سرعت عملکرد الگوریتم ایجاد نمی‌کنند. اگرچه عناصر کوچک نزدیک به آخر فهرست (که باید به سمت ابتدای فهرست بیایند) بسیار کند حرکت می‌کنند. این تفاوت در سرعت به حدی است که به عناصر بزرگ، خرگوش‌ها، و به عناصر کوچک، لاک‌پشت‌ها می‌گویند.
تلاش بسیاری انجام شده که سرعت حرکت لاک پشت‌ها در مرتب سازی حبابی افزایش یابد. از جمله می‌توان از [Cocktail Sort] نام برد که در این زمینه بسیار خوب عمل می‌کند ولی بدترین زمان اجرای آن هنوز (O(n^2 است. [مرتب سازی شانه‌ای] عناصر بزرگ با فاصله‌های زیاد را مقایسه می‌کند و لاک پشت‌ها را با سرعت فوق العاده‌ای حرکت می‌دهد سپس با کم تر و کم تر کردن این فاصله‌ها فهرست را به سرعت مرتب می‌کند، به طوری که سرعت متوسط آن قابل مقایسه با الگوریتم‌های پر سرعتی مثل مرتب سازی سریع می‌باشد.

مثال قدم به قدم

اجازه بدهید یک آرایه از عددهای “۵, ۱, ۴, ۲, ۸” اختیار کنیم و آن را به ترتیب صعودی با استفاده از مرتب سازی حبابی مرتب کنیم. در هر مرحله عناصری که در حال مقایسه شدن با یکدیگر هستند پر رنگ تر نشان داده شده‌اند:

گذر اول:

(۱, ۵, ۴, ۲, ۸) <= (۵, ۱, ۴, ۲, ۸)
در اینجا الگوریتم دو عنصر اول را مقایسه، و جابجا می‌کند.
(۱, ۴, ۵, ۲, ۸) <= (۱, ۵, ۴, ۲, ۸)
(۱, ۴, ۲, ۵, ۸) <= (۱, ۴, ۵, ۲, ۸)
(۱, 4, 2, ۵, ۸) <= (۱, ۴, ۲, ۵, ۸)
حالا آرایه مرتب شده‌است، ولی الگوریتم هنوز نمی‌داند که این کار کامل انجام شده‌است یا نه، که برای فهمیدن احتیاج به یک گذر کامل بدون هیچ جابجایی (swap) داریم:
گذردوم
(۱, ۲, ۴, ۵, ۸) <= (۱, ۲, ۴, ۵, ۸)
(۱, ۲, ۴, ۵, ۸) <= (۱, ۲, ۴, ۵, ۸)
(۱, ۲, ۴, ۵, ۸) <= (۱, ۲, ۴, ۵, ۸)
(۱, ۲, ۴, ۵, ۸) <= (۱, ۲, ۴, ۵, ۸)
در نهایت آرایه مرتب شده‌است و الگوریتم می‌تواند پایان پذیرد.

پیاده سازی شبه کد

بیان سادهٔ شبه کد مرتب‌سازی حبابی:

procedure bubbleSort(A: list of sortable items) defined as:
do
swapped:= false
for each i in 0 to length(A) - 2 inclusive do:
if A[ i ] > A[ i + 1 ] then
swap(A[ i ], A[ i + 1 ])
swapped:= true
end if
end for
while swapped
end procedure

پیاده سازی مرتب سازی حبابی در ++C

سورس مرتب سازی حبابی به زبان c++ به شرح زیر است:

1. include<iostream.h>

#include<conio.h>

void main()

{

clrscr();

int a[10],i,j,temp;

char ch;

for(i=0;i<10;i++)

cin>>a[i];

for(i=9;i>=0;i--)

for(j=0;j<=i;j++)

if(a[j]>a[j+1])

{

temp=a[j];

a[j]=a[j+1];

a[j+1]=temp;

}

for(i=0;i<10;i++)

cout<<a[i];

getch();

}

مثالی از مرتب سازی:

این سورس یک عدد گرفته و به تعداد همان عدد از ورودی دریافت می‌کند و آنها را با روش Bubble sort مرتب می‌کند .

#include<stdio.h>
#include<conio.h>
#include<stdlib.h>

//--------------------------------------------------------------------------
void read_list(int a[],int n){
 int i;
 for(i=0;i<n;i++){
  printf("\n\n\t ENTER THE ELEMENT [%d] :: ",i);
  scanf("%d",&a[i]);
 }
}
//--------------------------------------------------------------------------
void print_list(int a[],int n){
 int i;
 for(i=0;i<n;i++)
   printf("\t%d",a[i]);
}
//--------------------------------------------------------------------------
void bubble_sort(int a[],int n){
 int i,j,temp;
 for(i=0;i<n-1;i++){
  for(j=0;j<n-1;j++)
   if(a[j]>a[j+1]){
    temp=a[j];
    a[j]=a[j+1];
    a[j+1]=temp;
   }
  printf("\n\n\t PASS %d :: ",i);
  print_list(a,n);
 }
}
//--------------------------------------------------------------------------
void main(){
 int a[20],n;
 clrscr();
 printf("\n\n\t ENTER THE ARRAY LENGTH :: ");
 scanf("%d",&n);

 read_list(a,n);

 printf("\n\n\t THE ARRAY ELEMENTS ARE AS FOLLOWS :: ");
 print_list(a,n);

 bubble_sort(a,n);

 printf("\n\n\t THE SORTED LIST IS :: ");
 print_list(a,n);
 getch();
}
//--------------------------------------------------------------------------

تحلیل

نمونه‌ای از مرتب‌سازی حبابی که فهرستی از عددهای تصادفی را مرتب می‌کند.

بدترین حالت

این الگوریتم در بدترین حالت از مرتبهٔ (n^۲) است. چون در بدترین حالت هر عنصر باید n-1 بار فهرست را بپیماید.

بهترین حالت

بهترین حالت این است که فهرست مرتب شده‌باشد که در این حالت الگوریتم از مرتبه O(n) است.

دیگر روش‌های پیاده سازی

کارایی مرتب سازی حبابی با رعایت شرایط زیر می‌تواند افزایش قابل ملاحظه‌ای داشته باشد.
اول این که توجه داشته باشید بعد از هر مقایسه (و احتمالا جابجایی) در هر پیمایش، بزرگ‌ترین عنصری که از آن عبور می‌کنیم در آخرین موقعیت پیمایش شده قرار خواهد گرفت. از این رو بهد از اولین پیمایش بزرگ‌ترین عنصر آرایه در آخرین خانه آن خواهد بود.
این یعنی با داشتن فهرستی با اندازه n، پس از اولین پیمایش، n-امین عنصر در مکان نهایی اش خواهد بود. بنا بر استقرا بقیه n-1 عنصر باقیمانده به همین صورت مرتب می‌شوند که بعد از پیمایش دوم، n-1 امین عنصر در جای نهایی خودش خواهد بود، و الی آخر. پس طول هر پیمایش می‌تواندبه اندازه یک مرحله کم تر از پیمایش قبل از خودش باشد و به جای آنکه هر بار تمامی عناصر را تا انتهای آرایه بپیماییم، عناصری که در موقعیت پایانی خود هستند و از به هیچ عنوان جابجا نمی‌شوند چشم پوشی کنیم.
با تبدیل این روش به شبه کد خواهیم داشت:

procedure bubbleSort(A: list of sortable items) defined as:
  n:= length(A)
  do
    swapped:= false
    n:= n - 1
    for each i in 0 to n - 1  inclusive do:
      if A[ i ] > A[ i + 1 ] then
        swap(A[ i ], A[ i + 1 ])
        swapped:= true
      end if
    end for
  while swapped
end procedure

زمان اجرای این روش هنوز هم (O(n^2 است ولی در بدترین حالت (وقتی آرایه ورودی به صورت معکوس مرتب شده باشد) زمان اجرای آن دو برابر سریع تر از حالت عادی الگوریتم می‌باشد.

نمونه‌ای از عددهای تصادفی که به وسیله‌ٔ مرتب‌سازی زوج-فرد مرتب می‌شوند.