الگوریتم جستجوی عمقی (DFS)
به نام خدا
از title این پست کاملا معلومه که می خوایم در مورد چی حرف بزنیم ، (DFS !!!!)
بنابراین مستقیم میریم سر اصل مطلب. ( بفرمایید ادامه مطلب : )
الگوریتم از ریشه شروع میکند (در گرافها و یا درختهای بدون ریشه راس دلخواهی به عنوان ریشه انتخاب میشود) و در هر مرحله همسایههای رأس جاری را از طریق یالهای خروجی رأس جاری به ترتیب بررسی کرده و به محض روبهرو شدن با همسایهای که قبلاً دیده نشده باشد، به صورت بازگشتی برای آن رأس به عنوان رأس جاری اجرا میشود. در صورتی که همهٔ همسایهها قبلاً دیده شده باشند، الگوریتم عقبگرد میکند و اجرای الگوریتم برای رأسی که از آن به رأس جاری رسیدهایم، ادامه مییابد. به عبارتی الگوریتم تا آنجا که ممکن است، به عمق بیشتر و بیشتر میرود و در مواجهه با بن بست عقبگرد میکند. این فرایند تامادامیکه همهٔ رأسهای قابل دستیابی از ریشه دیده شوند ادامه مییابد.
همچنین در مسائلی که حالات مختلف متناظر با رئوس یک گرافاند و حل مسئله مستلزم یافتن رأس هدف با خصوصیات مشخصی است، جستجوی عمق اول به صورت غیرخلاق عمل میکند. بدینترتیب که هر دفعه الگوریتم به اولین همسایهٔ یک رأس در گراف جستجو و در نتیجه هر دفعه به عمق بیشتر و بیشتر در گراف میرود تا به رأسی برسد که همهٔ همسایگانش دیده شدهاند که در حالت اخیر، الگوریتم به اولین رأسی بر میگردد که همسایهٔ داشته باشد که هنوز دیده نشده باشد. این روند تا جایی ادامه مییابد که رأس هدف پیدا شود و یا احتمالاً همهٔ گراف پیمایش شود. البته پیادهسازی هوشمندانهٔ الگوریتم با انتخاب ترتیب مناسب برای بررسی همسایههای دیده نشدهٔ رأس جاری به صورتی که ابتدا الگوریتم به بررسی همسایهای بپردازد که به صورت موضعی و با انتخابی حریصانه به رأس هدف نزدیکتر است، امکانپذیر خواهد بود که معمولاً در کاهش زمان اجرا مؤثر است.
از نقطه نظر عملی، برای اجرای الگوریتم، از یک پشته (stack) استفاده میشود.(برای همین تو پست قبلی پشته رو گفتم .!!!) بدین ترتیب که هر بار با ورود به یک رأس دیده نشده، آن رأس را در پشته قرار میدهیم و هنگام عقبگرد رأس را از پشته حذف میکنیم. بنابراین در تمام طول الگوریتم اولین عنصر پشته رأس در حال بررسی است. جزئیات پیادهسازی در ادامه خواهد آمد.
وقتی در گرافهای بزرگی جستجو میکنیم که امکان ذخیرهٔ کامل آنها به علت محدودیت حافظه وجود ندارد، در صورتی که طول مسیر پیمایش شده توسط الگوریتم که از ریشه شروع شده، خیلی بزرگ شود، الگوریتم با مشکل مواجه خواهد شد. در واقع این راهحل ساده که "رئوسی را که تا به حال دیدهایم ذخیره کنیم" همیشه کار نمیکند. چراکه ممکن است حافظهٔ کافی برای این کار نداشته باشیم. البته این مشکل با محدود کردن عمق جستجو در هر بار اجرای الگوریتم حل میشود که در نهایت به الگوریتم تعمیق تکراری (Iterative Deepening) خواهد انجامید.
int w
Visited[v]:=1
For (each vertex w adjacent to v)
If (not visited[w]) then
DFS(w)
End if
End For
پیمایش با انتخاب رأس  به عنوان ریشه آغاز میشود.
به عنوان ریشه آغاز میشود.  به عنوان یک رأس دیده شده برچسب میخورد. رأس دلخواه
به عنوان یک رأس دیده شده برچسب میخورد. رأس دلخواه 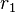 از همسایگان
از همسایگان  انتخاب شده و الگوریتم به صورت بازگشتی از
انتخاب شده و الگوریتم به صورت بازگشتی از 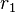 به عنوان ریشه ادامه مییابد.از این پس در هر مرحله وقتی در رأسی مانند
به عنوان ریشه ادامه مییابد.از این پس در هر مرحله وقتی در رأسی مانند  قرار گرفتیم که همهٔ همسایگانش دیده شدهاند، اجرای الگوریتم را برای آن
رأس خاتمه میدهیم. حال اگر بعد از اجرای الگوریتم با ریشهٔ
قرار گرفتیم که همهٔ همسایگانش دیده شدهاند، اجرای الگوریتم را برای آن
رأس خاتمه میدهیم. حال اگر بعد از اجرای الگوریتم با ریشهٔ 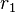 همهٔ همسایگان
همهٔ همسایگان  برچسب خورده باشند، الگوریتم پایان مییابد. در غیر این صورت رأس دلخواه
برچسب خورده باشند، الگوریتم پایان مییابد. در غیر این صورت رأس دلخواه 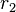 از همسایگان
از همسایگان  را که هنوز برچسب نخورده انتخاب میکنیم و جستجو را به صورت بازگشتی از
را که هنوز برچسب نخورده انتخاب میکنیم و جستجو را به صورت بازگشتی از 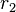 به عنوان ریشه ادامه میدهیم. این روند تامادامیکه همهٔ همسایگان
به عنوان ریشه ادامه میدهیم. این روند تامادامیکه همهٔ همسایگان  برچسب نخوردهاند ادامه مییابد.
برچسب نخوردهاند ادامه مییابد.
این مطلب از سایت wikipedia بود ، چون خیلی قشنگ و کامل توضیح داده بود ،
اگه علاقه مندید بیشتر بخونید ، به خود wiki مراجعه کنید.
ممنون.
خدا نگهدار.


