برنامه نویسی پویا چیست؟

یکی از روش‌های پرکاربرد و مشهور طراحی الگوریتم روش برنامه‌نویسی پویا (یا برنامه‌ریزی پویا - Dynamic Programming) است. این روش همچون روش تقسیم و حل (Divide and Conquer) بر پایه تقسیم مساله بر زیرمساله‌ها کار می‌کند. اما تفاوت‌های چشم‌گیری با آن دارد.

زمانی که یک مساله به دو یا چند زیرمساله تقسیم می‌شود، دو حالت ممکن است پیش بیاید:

1- داده‌های زیرمساله‌ها هیچ اشتراکی با هم نداشته و کاملا مستقل از هم هستند. نمونه چنین مواردی مرتب‌سازی آرایه‌ها با روش ادغام یا روش سریع است که داده‌ها به دو قسمت تقسیم شده و به صورت مجزا مرتب می‌شوند. در این حالت داده‌های یکی از بخش‌ها هیچ ارتباطی با داده‌های بخش دیگر نداشته و در نتیجه حاصل از  آن بخش اثری ندارند. معمولا روش تقسیم و حل برای چنین مسائلی کارآیی خوبی دارد.

2- داده‌های زیرمساله وابسته به هم بوده و یا با هم اشتراک دارند. در این حالت به اصطلاح زیرمساله‌ها هم‌پوشانی دارند. نمونه بارز چنین مسائلی محاسبه جمله nام دنباله اعداد فیبوناچی است.

 

دنباله اعداد فیبوناچی (فیبوناتچی)

دنباله اعداد فیبوناچی (Fibonacci) یکی از دنباله‌های عددی مشهور ریاضیات با تعریف بازگشتی زیر است:

 

F( n ) = F( n - 1 ) + F( n - 2 )      n > 2      ,      F( 1 ) = F( 2 ) = 1

 

محاسبه جمله nام دنباله به محاسبه دو جمله قبلی آن نیاز دارد. پس می‌توان گفت محاسبه ( F( n - 1  و ( F( n - 2 دو زیر مساله برای مساله اصلی هستند. اما در عین حال این دو زیرمساله از هم مستقل نیستند. برای محاسبه ( F( n - 1 بر اساس رابطه بالا باید داشته باشیم:

 

F( n - 1 ) = F( n - 2 ) + F( n - 3 )

 

که نشان می‌دهد خود ( F( n - 1 وابسته به ( F( n - 2 است.

اگر این مساله را به روش تقسیم و حل - که ساده‌ترین روش است - حل کنیم:

 

int fibo( int n )

{

  if( n > 2 )

  {

    return ( fibo( n - 1) + fibo( n - 2 ) );

  }

  return 1;

}

 

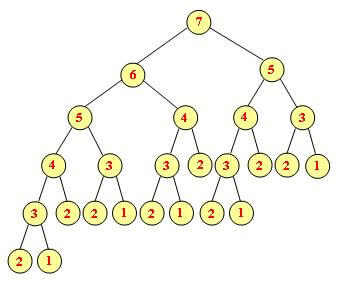
تابع fibo مقدار n را دریافت کرده و به صورت بازگشتی و بر اساس رابطه ذکر شده، جمله nام دنباله فیبوناچی را محاسبه می‌کند. حال درخت فراخوانی‌های بازگشتی تابع را به ازای n = 7 رسم می‌کنیم:

 

 

 

هر گره درخت، فراخوانی تابع را با مقدار داخل آن نشان می‌دهد. برای محاسبه جمله هفتم دنباله فیبوناچی تابع fibo به صورت ( fibo( 7 فراخوانی می‌شود، که آن هم ( fibo( 6 و ( fibo( 5 را فراخوانی می‌کند و الی آخر. همانطور که مشاهده می‌کنید، برای محاسبه این جمله، ( fibo( 7 یک بار، ( fibo( 6 یک بار، ( fibo( 5 دو بار، ( fibo( 4 سه بار، ( fibo( 3 پنج بار، ( fibo( 2 هشت بار، ( fibo( 1 پنج بار، و روی هم رفته تابع fibo بیست و پنج بار فراخوانی می‌شود.

ما خود چگونه جملات دنباله فیبوناچی را محاسبه می‌کنیم؟ ابتدا جمله اول و دوم را جمع زده و جمله سوم را محاسبه می‌کنیم. سپس با استفاده از جمله به دست آمده و جمله دوم، جمله چهارم را محاسبه می‌کنیم و همینطور ادامه می‌دهیم:

 

1  1  2( = 1 + 1 )

1  1  2  3( = 2 + 1 )

1  1  2  3  5( = 3 + 2 )

1  1  2  3  5  8( = 5 + 3 )

1  1  2  3  5  8  13( = 8 + 5 )

 

و به این ترتیب جمله هفتم دنباله تنها با پنج محاسبه ساده به دست می‌آید. در حالت کلی با استفاده از این روش تنها به n - 2 عمل جمع نیاز است که نشان از الگوریتمی با مرتبه خطی دارد. در حالی که می‌توان ثابت کرد در حالت اول تعداد کل فراخوانی‌های بازگشتی تابع از مرتبه نمایی است. دلیل اختلاف این دو عدد در این است که در حالت دوم، هر جمله دنباله فقط و فقط یک بار محاسبه می‌شود. این همان روش برنامه‌نویسی پویا است.

در برنامه‌نویسی پویا مساله به صورت جزء به کل حل می‌شود. یعنی ابتدا زیر مسائل خرد حل شده و نتیجه آنها در مکانی دخیره می‌شود. سپس به سمت زیرمسائل کلی‌تر رفته و با استفاده از داده‌های از پیش محاسبه شده، آنها نیز حل می‌شوند. در مورد دنباله فیبوناچی می‌توان نوشت:

 

int fibo( int n )

{

  int f[ MAX ], i;

  f[ 1 ] = f[ 2 ] = 1;

  for( i = 3 ; i <= n ; i++ )

  {

    f[ i ] = f[ i - 1 ] + f[ i - 2 ];

  }

  return f[ n ];

}

 

در این روش ما جملات دنباله‌ها را پس از محاسبه در یک آرایه ذخیره می‌کنیم. برای این کار به جای حرکت از کل به جزء (یعنی از n به 1، که در روش تقسیم و حل استفاده می‌شود)، از جزء به سمت کل حرکت می‌کنیم. هر جمله دنباله تنها به دو جمله قبل خود نیاز دارد، که با حرکت جزء به کل قبلا محاسبه شده‌اند و نیاز به محاسبه مجدد آنها نیست. البته این کد را می‌توان ساده‌تر کرد:

 

int fibo( int n )

{

  int i, f1, f2, f3;

  f1 = f2 = 1;

  for( i = 3 ; i <= n ; i++ )

  {

    f3 = f1 + f2;

    f1 = f2;

    f2 = f3;

  }

  return f3;

}

 

تحلیل این تابع ساده را به خود شما وا می‌گذارم.

نکته مهم این است که اگر زیرمساله‌ها هم‌پوشانی نداشته باشند روش برنامه‌نویسی پویا هیچ کمکی به ما نخواهد کرد. چرا که خاصیت اصلی این روش ذخیره داده‌هایی است که ممکن است به کرات به آنها مراجعه شود. حال اگر هیچ اشتراکی در کار نباشد، طبیعتا از هر داده تنها یک بار استفاده خواهد شد.

برنامه‌نویسی پویا برای طراحی الگوریتم‌های محاسبه حالت‌های بهینه مسائل نیز کاربرد زیادی دارد. به عنوان مثال در یافتن کوتاهترین مسیر بین دو نقطه، محاسبه بهینه‌ترین حالت ضرب زنجیری ماتریس‌ها، درخت جستجوی بهینه، مساله فروشنده دوره‌گرد، محاسبه ضرب چندجمله‌ای‌ها، مساله کوله‌پشتی صفر و یک، و چندین مساله دیگر، از برنامه‌نویسی پویا استفاده می‌شود. شرط اساسی امکان استفاده از این روش برای محاسبه حالت بهینه به اصل بهینگی مشهور است.

اصل بهینگی: اصل بهینگی یعنی حل مساله به صورت بهینه، حاوی حل بهینه تمامی زیرمسائل آن نیز باشد.

به عبارت دیگر، مساله باید به گونه‌ای باشد که با یافتن حل بهینه آن، حل بهینه همه زیرمساله‌ها نیز به دست آمده باشد. به عنوان مثال، در یافتن کوتاهترین مسیر بین دو شهر، مسیر بین مبدا و هر گرهی که در مسیر بهینه وجود دارد، بهینه‌ترین مسیر بین آن دو نیز هست.