درخت heap

آموزش درخت heap

درخت دودویی کامل

یک درخت دودویی کامل است، هرگاه تمامی سطوح درخت به غیر از احتمالا آخرین سطح پر بوده، و برگ‌های سطح آخر از سمت چپ قرار گرفته باشند.

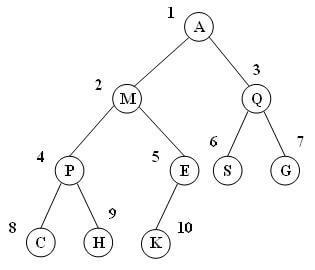
به یک مثال دقت کنید: 

 

 

همانطور که مشاهده می‌کنید، تمامی سطوح درخت به غیر از آخرین سطح به طور کامل پر و همه برگ‌های سطح آخر نیز در سمت چپ درخت هستند. در واقع تمامی برگ‌های درخت دودویی کامل در دو سطح آخر آن قرار دارند.

 

نمایش درخت دودویی کامل

نمایش با استفاده از لیست پیوندی و آرایه دو شکل مشهور نمایش درخت دودویی در ساختمان داده‌ها است. در حالت عادی انتخاب یکی از این دو روش برای نمایش بهینه و با مصرف حافظه کمتر بسته به چیدمان عناصر درخت دارد. به عنوان مثال، در درخت‌های مورب روش نمایش با آرایه بدترین بازدهی و بیشترین مصرف حافظه را دارد. اما در درخت دودویی کامل این روش در مقایسه با روش لیست پیوندی بسیار بهینه‌تر است.

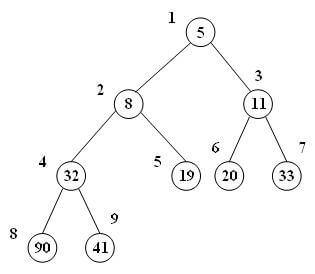
در روش استفاده از آرایه برای نمایش درخت دودویی، گره‌های درخت مطابق شکل فوق با شروع از ریشه و در هر سطح از چپ به راست به ترتیب شماره‌گذاری شده و مقدار هر کدام از گره‌ها با توجه به شماره آن در یکی از خانه‌های آرایه قرار می‌گیرد. برای درخت فوق داریم:

 

 

در آرایه متناظر درخت دودویی کامل، از همه عناصر به صورت کامل استفاده شده و هیچ حافظه هرزی وجود ندارد (چرا؟). به همین خاطر، این روش نمایش برای درخت کامل مناسب است.

فرض کنیم توابع Left ،Parent و Right شماره یک گره را گرفته و به ترتیب شماره گره والد، فرزند چپ و فرزند راست را برگرداند. در این صورت با توجه به شکل فوق:

 

Parent( i ) = [ i / 2 ]     ,     Left( i ) = 2 i     ,     Right( i ) = 2 i + 1

 

که منظور از [ ] جزء صحیح (کف) عدد است.

به عنوان مثال، در مورد گره شماره 3 می‌توان نوشت:

 

Parent( 3 ) = [ 3 / 2 ] = 1     ,     Left( 3 ) = 2 x 3 = 6     ,     Right( 3 ) = 2 x 3 + 1 = 7

 

هرم ماکزیمم (ماکس هیپ / max-heap)

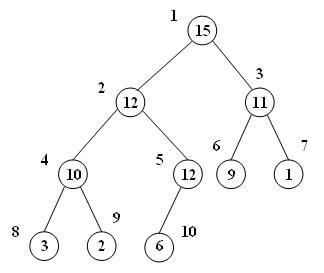
درخت دودویی کاملی است که مقدار هر گره بیشتر یا مساوی فرزندان خود است.

 

 

 

و نمایش آرایه‌ای:

  

  

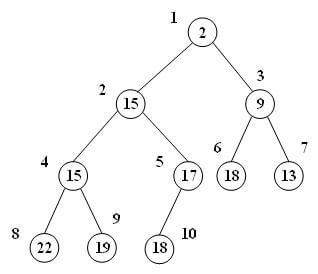
هرم مینیمم (مین هیپ / min-heap)

درخت دودویی کاملی است که مقدار هر گره کمتر یا مساوی فرزندان خود است.

 

 

و نمایش آرایه‌ای:

 

 

 

ساختن درخت Heap

 ساختن یک درخت heap در واقع وارد کردن متوالی گره‌ها در آن است. برای وارد کردن یک گره به درخت heap، طی دو مرحله به صورت زیر عمل می‌کنیم:

1- گره مفروض را در محلی از درخت که شرط کامل بودن آن به هم نخورد (بدون در نظر گرفتن شرط max-heap یا min-heap بودن) درج می‌کنیم.

2- اگر گره مذکور بر اساس موقعیت خود در درخت، شرط max-heap یا min-heap بودن را نقض نکند، نیاز به انجام کاری نیست و عملیات درج تمام شده است. در غیر اینصورت، با جابجا کردن گره با والد خود، درخت جدیدی حاصل می‌شود که باید مرحله 2 در مورد آن تکرار شود.

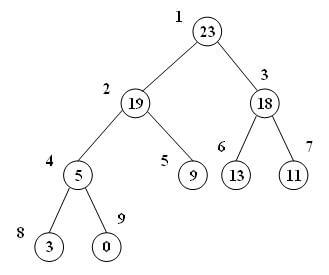
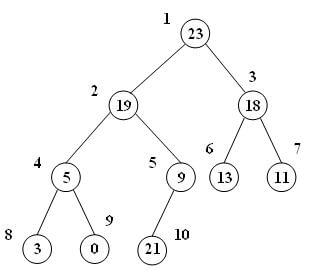
به عنوان مثال، فرض کنید یک درخت max-heap به فرم زیر داریم:

 

 

حال می‌خواهیم گرهی با مقدار 21 را به درخت اضافه کنیم. برای اینکار در مرحله اول گره مذکور را به محلی که شرط کامل بودن درخت نقض نشود وارد می‌کنیم. این محل سمت چپ‌ترین فضای آزاد آخرین سطح درخت است:

 

 

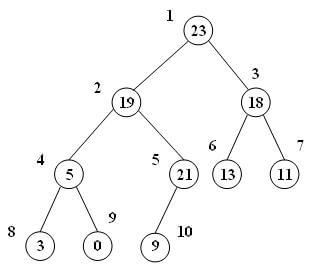
با درج این گره، شرط max-heap بودن نقض می‌شود. چرا که مقدار گره شماره 10 از والد خود یعنی گره شماره 5 بیشتر است. پس با توجه به دستورالعمل مرحله دوم، مقدار دو گره را جابجا می‌کنیم:

 

 

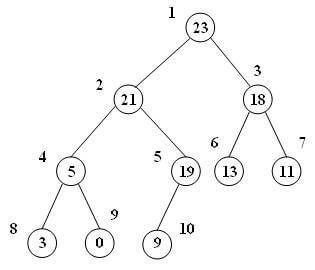
با این عمل، باز هم شرط max-heap بودن برآورده نمی‌شود. گره‌های شماره 5 و 2 این شرط را نقض کرده‌اند. پس باز هم با تکرار مرحله دوم مقدار این دو گره را با هم جابجا می‌کنیم:

 

 

حال شرط max-heap بودن برقرار بوده و عملیات درج گره تمام می‌شود.

با توجه به این مثال می‌توان مرحله دوم عملیات درج را اینگونه بیان کرد:

2- گره درج شده را با والدهای خود تا جایی که شرط max-heap یا min-heap بودن برقرار شود جابجا می‌کنیم.

 

برنامه‌نویسی درج گره در درخت heap

در اینجا کد مربوط به درج گره در درخت max-heap را می‌آورم، که با یک تغییر جزئی همین کد برای درخت min-heap هم قابل استفاده است.

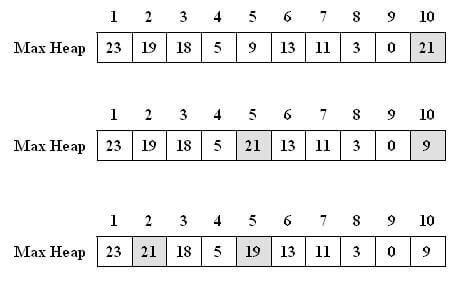
همانطور که بحث شد، بهترین روش نمایش درخت heap استفاده از آرایه است. در مورد درخت max-heap اولیه فوق داریم:

 

 

با اضافه کردن گره 21 و طی کردن مراحل دوگانه درج گره:

 

 

در قسمت قبلی رابطه ریاضی بین اندیس‌های والد و فرزند بیان شده است. بر اساس این رابطه و توضیحات فوق، تابع درج گره با مقدار v در یک درخت max-heap که در حال حاضر n عنصر (گره) دارد در زبان ++C به این صورت خواهد بود:

 

void push( int heap[ ], int &n, int v )

{

    int i, temp;

    heap[ ++n ] = v;

    for( i = n ; i > 1 && heap[ i ] > heap[ i / 2 ] ; i /= 2 )

    {

        temp = heap[ i ];

        heap[ i ] = heap[ i / 2 ];

        heap[ i / 2 ] = temp;

    }

}

 

تذکر 1: اندیس آرایه‌ها در زبان برنامه نویسی ++C از صفر شروع می‌شود. اما در اینجا برای راحتی کار و هماهنگ شدن با روش شماره‌گذاری درخت دودویی کامل، از اولین خانه - یعنی خانه شماره صفر - برای نمایش درخت heap استفاده نشده است.

تذکر 2: در این تابع پارامتر n به صورت مرجع تعریف شده است که مختص زبان برنامه‌نویسی ++C بوده و در زبان C وجود ندارد. متغیرهای مرجع در یک مطلب آموزشی به طور کامل توضیح داده شده است.

نکته: روش درج گره جدید در درخت heap در ظاهر شباهت‌هایی به درج گره جدید در درخت جستجوی دودویی (Binary Search Tree) دارد. اما این دو اختلاف‌های مشخصی دارند:

• در درخت جستجوی دودویی برای یافتن محل مناسب گره، از ریشه به سمت برگ، اما در درخت هیپ، از برگ به سمت ریشه حرکت می‌کنیم.
• در درخت جستجوی دودویی گره‌ها را برای یافتن مکان مناسب گره جدید بدون هیچگونه عمل جابجایی پیمایش می‌کنیم؛ و تنها زمانی که محل مورد نظر یافت شد عمل درج انجام می‌شود. اما در درخت هیپ، گره از همان ابتدا درج شده، و سپس با جابجایی با والدهای خود، محل مناسب آن پیدا می‌شود.

 

نکته: با توجه به قطعه کد بالا، مرتبه اجرایی عمل درج در درخت heap از مرتبه ( O( log n است.

 

حذف گره از درخت Heap

حذف گره از درخت هیپ عموما از ریشه آن صورت می‌گیرد. حذف گرهی غیر از گره ریشه، ممکن است هزینه‌ای معادل ساخت مجدد درخت تحمیل کند. چرا که با حذف یک گره غیر ریشه و جایگزین کردن گرهی دیگر با آن، نه تنها شرط heap بودن، که شرط درخت کامل بودن هم ممکن است نقض شود. اکثر کاربردهای این نوع درخت نیز تنها با حذف گره از ریشه سر و کار دارند.

برای حذف گره ریشه درخت دو مرحله زیر را اجرا می‌کنیم:

1- گره ریشه را حذف و سمت راست‌ترین برگ سطح آخر را جایگزین آن می‌کنیم.

2- در صورتی که گره درج شده جدید شرط heap بودن را نقض نکند عملیات حذف تمام می‌شود. در غیر اینصورت این گره با فرزند مناسب جایگزین شده و این مرحله برای درخت جدید مجددا اجرا می‌شود.

با اجرای مرحله اول و جایگزین کردن آخرین گره آخرین سطح درخت، شرط کامل بودن درخت پایدار می‌ماند. اما عموما شرط heap بودن نقض می‌شود. در مرحله دوم، گره تازه وارد را با یکی از فرزندان خود جایگزین می‌کنیم، تا به شرط heap بودن نزدیک شویم. اما کدام فرزند؟ پاسخ را با یک مثال مشخص می‌کنم.

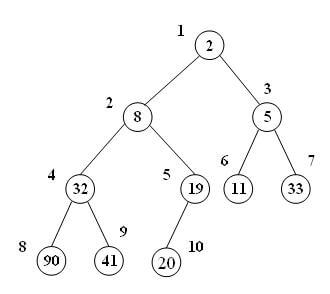
فرض کنید قصد داریم گره ریشه درخت min-heap زیر را حذف کنیم:

 

 

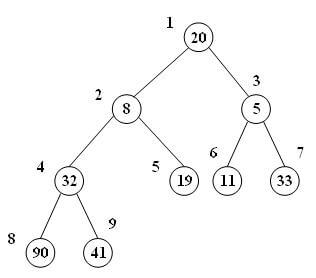
مرحله اول را اجرا کرده و گره شماره 10 را جایگزین ریشه می‌کنیم:

 

 

شرط درخت کامل بودن همچنان برقرار است. اما درخت فعلی min-heap نیست. چرا که ریشه از هر دو فرزند خود بزرگتر است. حال مطابق مرحله دوم باید یکی از فرزندان را با والد جابجا کنیم.

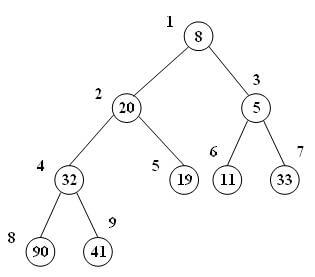
اگر فرزند چپ با مقدار 8 را انتخاب کنیم:

 

 

در این حالت، علاوه بر بحث مکان درست گره شماره 2 با مقدار 20، مشکل دیگری هم داریم: گره شماره 1 و 3 هم شرط min-heap را نقض می‌کنند.

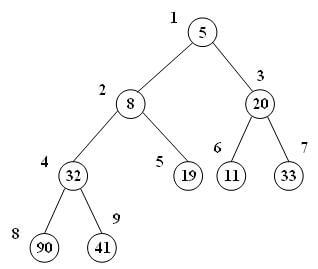
اگر فرزند راست را انتخاب می‌کردیم:

 

 

در این حالت لااقل گره‌های شماره 1 و 2 مشکلی ندارند و تنها دغدغه ما محل درست گره شماره 3 خواهد بود. پس نتیجه اینکه: در درخت min-heap، فرزندی را جایگزین والد می‌کنیم که مقدار کوچکتری داشته باشد. این مساله در مورد max-heap به صورت عکس است. یعنی فرزندی را در درخت max-heap جایگزین می‌کنیم که مقدار بیشتری دارد.

اما هنوز گره شماره 3 شرط min-heap بودن را نقض می‌کند. پس با تکرار مرحله دوم و با توجه به نتیجه‌گیری فوق، این گره را با گره شماره 6 جابجا می‌کنیم:

 

 

به این ترتیب شرط min-heap بودن نیز برقرار شده، و عملیات حذف گره به اتمام می‌رسد.

 

برنامه‌نویسی حذف گره از درخت heap

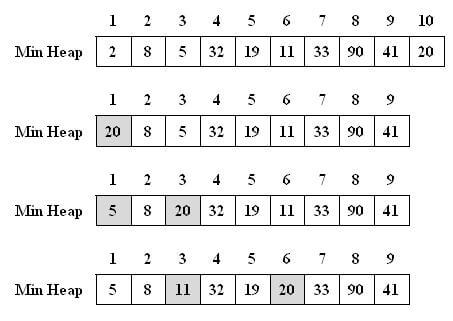
این عملیات برای درخت فوق در نمایش آرایه‌ای به فرم زیر خواهد شد:

 

 

بر اساس روابط ریاضی بین شماره اندیس گره‌های والد و فرزند، تابع pop برای حذف گره ریشه به این ترتیب خواهد بود:

 

int pop( int heap[ ], int &n )

{

    int i = 1, result, temp, min;

    result = heap[ 1 ];

    heap[ 1 ] = heap[ n-- ];

    while( 2 * i <= n )

    {

        min = 2 * i;

        if( min + 1 <= n && heap[ min + 1 ] < heap[ min ] )

        {

            min++;

        }

        if( heap[ i ] <= heap[ min ] )

        {

            break;

        }

        temp = heap[ i ];

        heap[ i ] = heap[ min ];

        heap[ min ] = temp;

        i = min;

    }

    return result;

}

 

توجه داشته باشید که تابع pop درخت heap به فرم آرایه و تعداد عناصر آن را دریافت کرده و ضمن حذف گره ریشه، مقدار آن را باز می‌گرداند.

 

نکته: با توجه به قطعه کد بالا، مرتبه اجرایی عمل حذف گره از درخت heap از مرتبه ( O( log n است.

 

برگرفته از: الگوریتم ها